Topic # 07

Astrophysical Evidence shows Profound Fundamental Principles of Mathematical Physics

have been misapplied to Current Concepts of Gravitational Lensing.

updated 17 October 2007

Abstract

Examination of the literature in many renown refereed journals consistently shows that some very important fundamental principles in Mathematical Physics have been seriously misapplied to prevailing concepts in Gravitational lensing or just simply ignored. The fundamental principle known as Gauss' law, applied to gravitational fields for a point mass particle enclosed inside of an analytical Gaussian sphere, analogous  to the Gauss' law in Electrodynamics which is applied to an electric field of a point charge enclosed inside of a analytical Gaussian sphere. The Gauss' law serves as a very important guide for the understanding of complicated problems. This important fundamental principle is scarcely applied or simply misapplied in the publications on gravitational lensing.  Another important fundamental principle is that of the principle of optical reciprocity, an essential tool for the understanding of complex optical lens systems and techniques for the treatment of optical light rays. Major publications in renown refereed journals on the subject matter of gravitational lensing all too often present artist depictions on how a distorted image might appear due to gravitational effects on the emitted light. The illustrations and artist depictions are all often not based on sound fundamental reasoning supported by principles taught in modern academia. This study finds that an intensely observed phenomena in modern Astrophysics, believed to be good prospects for the detection of gravitational lensing, are too often not treated with the important fundaments which are scarcely applied or simply misapplied in the publications. For this reason, the astrophysical observations at Sagittarius A*, a region located at the galactic center of the Milky Way, has been seriously misinterpreted. This will be the focal point of this discussion. 

Details

The past decades of intense observations using modern astronomical techniques in Astrophysics reveals an obvious lack of evidence for lensing effects on the collected emissions from sources orbiting about Sagittarius A*, a super massive object thought to be a black hole located at the galactic center of the Milky Way. Significant findings reveal apparent misapplications of known fundamental to the observations by astrophysicists in an attempt to estimate the effect of gravitation on rays of light from Sagittarius A*.

The important points here are that the fundamental principles of Mathematical Physics,

•  the fundamental principle of analytical Gaussian Surface Law, applied to gravitation as well as to electromagnetism and
•  the fundamental principle of optical reciprocity

have been virtually ignored or misapplied. These fundamental principles clearly show

• that a co-linear alignment of the observer, the lens and the source  

is totally unnecessary for any observation of a light bending effect, as would be predicted by the light bending rule of General Relativity.

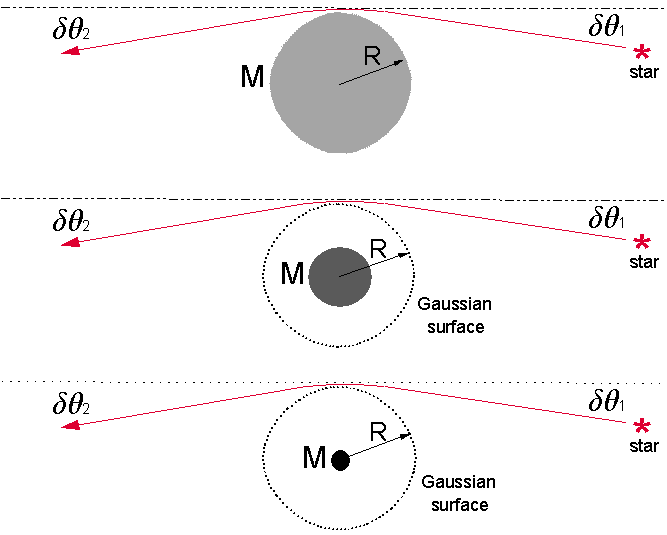
Any gravitational effect that would be observed in the vicinity of a gravitating mass at an impact parameter R for a given light ray would theoretically depend on the amount of Mass M that is enclosed within the analytical Gaussian sphere of radius R as illustrated in Fig 1.

Fig 1  Gauss' Surface Law of Gravitating Mass Enclosed 

The gravitational effect that would be noted at the surface of an analytical Gaussian sphere does not care at all about the size or radius of the mass that is enclosed within the sphere. We can see from Gauss's Law that equal masses of different radii will have theoretically equal gravitational effects at an analytical Gaussian surface of radius R. The gravitational effect outside of an analytical Gaussian surface does not care at all about the size or radius of the mass that is enclosed within the Gaussian surface. We can see from Gauss's Law that equal masses of different radii will theoretically have equal gravitational effects at the surface of the Gaussian sphere of radius R.

Fig 2 Symmetry Requirement of Lensing Demonstrated 

From Fig 2 the total deflection of the light ray, and thus the total angle of gravitational deflection representing the accumulative effect of gravitation on the light ray is give as

In this example the gravitating mass M is chosen to be positioned at the midpoint on the line of length D_S  joining the observer and the source. The astronomical distance D_L is the distance from the observer to the lens and  D_SLis the distance from the lens to the source. Also again, it is important to note that this case is only a simplified case, by setting D_L = D_SL, presented in most academic textbooks. There is no requirement at all that the lens be positioned exactly at the midpoint for an observation of a theoretical Einstein ring. Of course, this again would assume the validity of the light bending rule of General Relativity. This will become much more clearer in the next section that addresses the axis of symmetry of the lensed light ray for corresponding near- and far observers. It is readily seen that the axis of symmetry for a given light ray is perpendicular to the line joining the source and the observer only for the special case where the lens is positioned at the midpoint.

In this example, the radius R of the analytical Gaussian sphere enclosing the gravitating mass M is related to the angle h under which an astronomical object of that size might appear to an observer and is given by

where R and D_L are expressed in meters and the angle h is expressed in radians.  

The impact parameter for all the light rays that would be responsible for producing an image of an Einstein ring would simply be R. This is the nearest point of approach of the light rays to the center of the gravitating mass M. The gravitational effect on the light ray, on approach to the gravitating mass,  would then be

From symmetry we have

Since we are dealing with small angles, from Fig 2, the deflection of the light ray due to the gravitational effect on approach to the gravitating mass is just simply

Solving for the radius of the impact parameter of the light ray and thus the radius of the Einstein Ring expressed in radians we have

and finally

Note that the angle of deflection for the approach segment, one half of the total gravitational effect, is exactly equal to the radius of the solved Einstein ring expressed in radians and is given as   

This principle, an essential Mathematical Physics principle on lensing, is often totally missed by researchers attempting to deal with this topic. From symmetry requirement, the gravitational effect on a light ray upon approach to a gravitating mass positioned exactly at the midpoint of a line joining the source and the observer, must equal that of the gravitational effect on the light ray upon receding the gravitating mass.

This is a rarely covered fundamental on gravitational lensing in modern academic textbooks. The accumulative effect must sum the effects on the light ray upon approach and receding the gravitating mass. The total deflection is thus

Fig 3 Fundamental Principle of Optical Reciprocity of the Light Ray Illustrated

Irregardless of what one's position on gravitational lensing of light might be, the fundamental principle of optical reciprocity must hold. This is a given. The principle of optical reciprocity simply states and dictates that any light ray or a photon of light must take the very same path in either direction between the source and the observer. This is depicted in Fig 3.

Historically, the effect of light bending has been noted only at the solar rim, the thin plasma of the sun's atmosphere due to a refraction of the light by the solar plasma only.  This is a firm and well founded observational fact. Fig 4 illustrates the theoretical light bending effect of the sun at various radii of analytical Gaussian surfaces concentric to the center of the sun as suggested by General Relativity.

Fig 4 Gravitation light bending of the sun as function of integer solar Gaussian Surface radii

as predicted by General Relativity

We note again that the solar lensing is not at all midway between the star and the Earth based observer. Since the astronomical distances are extremely large, for all practical purposes, the gravitational effect on approach and on receding are virtually equal and the relation

still holds.

Remarkable as it may seem, however, historically the solar light bending effect has been observed only at the solar rim, the refractive plasma atmosphere of the sun. It is also important to note that, assuming the validity of the light bending rule of General Relative, the current technical means of the astronomical techniques should have easily allowed observations of solar light bending of stellar light rays at different solar radii of analytical Gaussian surfaces, namely at the radius of 2R, 3R and even at 4R, where R is one solar radius, as illustrated in Fig 4. For instance, at the analytical Gaussian surface of radius 2R, the predicted light bending effect of General Relativity would have been an easily detectable effect of one half the original effect; at the surface of radius 3R, an effect of one third the original effect, etc., etc.

It is widely taught in many Physics lectures that the solar light bending effect noted at the solar rim is done primarily to maximize the effect for detection and that gravitational lensing is most sensitive at the rim. This teaching also contributes to the misapplication of the important fundaments as well.  Note again, that the thickness of the solar rim is very negligible in comparison to the solar radius R.

The following animation illustrates the historically observed solar grazing effect of star light. Note, the thickness of the solar plasma is greatly exaggerated in this animated illustration.

Fig 5  Image from  

The images collected since 1992 from the orbiting stars about Sagittarius A* located at the galactic center have revealed absolutely NO distortions due to gravitational lensing effects as predict by General Relativity; NO evidence for gravitational light bending as illustrated in the recorded undistorted time resolved images of stellar objects orbiting about Sagittarius A*.

At the core of the Milky Way a major experiment in astrophysics is now brewing at this very moment. The past 10 years of astrophysical observations on the galactic core of the Milky Way reveal that the observed Kepler motion of the rapidly moving stars orbiting about Sagittarius A* appears to counter the predictions of General Relativity. The effect is understandable from a straight forward principle of Mathematical Physics that encloses the apparent galactic core mass inside of an analytical Gaussian spherical surface and from a principle of optical reciprocity on the path of a light ray that is predicted to bend under influence of the gravitating core mass as predicted by General Relativity. The principle of optical reciprocity simply states that the photons of light from any ray that joins the observer and the source would take exactly the same path in either direction. From the principle of equal gravitational effects for equal masses enclosed in an analytical Gaussian surface, it is clearly seen that a co-linear alignment of the observer, the lens and the source is totally unnecessary for any observation of a light bending effect predicted by General Relativity. A co-linear alignment is only a special case required for the Geometry of a perfectly constructed Einstein ring.

Any light ray that is gravitationally bent by a point-like gravitating mass, as is predicted by General Relativity, will always have an axis of symmetry which would be perpendicular to the line joining the source and the observer only when the lens is positioned exactly at the midpoint on the line joining the observer and the source.  This is depicted in the animated illustration in Fig 6.

Fig 6  Ray Dependency of Near- and Far-field Observers

It is readily seen that the far-field observer and the near-field observer will collect the light of a completely different set of rays, depending on the geometry of the ray lensing, each ray with a correspondingly distinct axis of symmetry. The problem is actually a 3-dimensional problem which assumes the light collected by the observer is a set of rays wrapped around the line joining the source and the observer. The observers depicted here, both the near-field observer and the far-field observer, should see a theoretical Einstein ring as predicted by General Relativity. The axis of symmetry is perpendicular to the line joining the source and the observer only when the lens is exactly at the midpoint on the line joining the source and the observer; the special simplified case, most often explained in the elementary Physics textbooks.  

IMPORTANT NOTE:

1) Light rays that do not cross can never produce an Einstein ring at the observer. 

2) All co-linearly positioned observers, near and far, should theoretically have a corresponding set of crossing light rays at his point of observation; an observable Einstein ring.

3) We have seen from the fundamental principle of the Gauss Law that an exact co-linear alignment of the observer, the lens and the source is not required for an observation of lensing. Thus, all observers depicted above, whether near or far, should theoretically be able to detect some lensing effects, if not a perfect ring, of course, assuming again the validity of General Relativity.

Some popular lensing tools frequently used by modern astrophysicists and gravitational lensing experts, as depicted in the figure below, apparently did not use the principle of optical reciprocity and consider the lensing effects in the vicinity of the lens in their design considerations. 

Fig 7A Ray Geometry Technique for Gravitational Lensing

Researchers utilizing this tool seek an alternative simplification for the application of the cumbersome light bending rule of General Relative and may or may not be thoroughly familiar with the basic principle of light bending of General Relativity given by the equation 

            (1)

derived using General Relativity considerations!  The geometry as well as the Physics of conservation of energy, the Physics of the minimum energy path, minimum time and the principle of reciprocity must all be considered for any correct interpretation of the astrophysical events.

From the above Figure,  "Ray Geometry Technique for Gravitational Lensing", the angle

           (2)

is derived. It is readily see that, as the source approaches the vicinity of the gravitational lens, where the adjustable parameter D_ds is the distance between the source and the lens and D_s = 26,000 light years, the distance between the observer and the source, the lensing estimated by this equation (2), a modification of  (1), approaches a very small value (approaches zero). This suggests incorrectly that the lensing effect described by (2) is minimized for sources in proximity to the gravitating mass, the lens.

It is important to note and recall that the principle of light bending of General Relativity given by Equation (1) and the Ray Geometry Technique for Gravitational Lensing given by Equation (2) are not the same equations, the main subject of the published paper.

Also note that the concept of micro-lensing may be a direct consequence of the misapplication of fundamental principles in optics and gravitation.

Fig 7B Einstein Ring Calculation: General Case to Text Book Special Case

Note that in most text books on the subject matter of the Einstein ring treats the overly simplified special case of the Einstein ring where the lens is depicted as being exactly midway between the observer and the light source. It is also important to note that the angular radius (radians) of the impact parameter, which is also a virtual ring itself, as depicted in Figure 7B, is the very same radius as the predicted Einstein ring. The radius (in meters) is simply equated to the radius (in radians) multiplies by the distance (in meters).

SOME ASTROPHYSICAL and OBSERVATIONAL EVIDENCE

Fig 8 Galaxy Pair NGC 3314: Rare image of two galaxies in exact line-of-site

from imgsrc.hubblesite.org

Astronomical data is available at:

It is readily seen that, in this rare exact line-of-site image in Constellation Hydra of the galaxy pair, that no apparent lensing is noted. The foreground galaxy NGC 3314a is roughly 117 million light-years (35 Mpc) away and the background galaxy NGC 3314b is roughly 140 million light-years (42 Mpc) away. (Position (J2000) RA 10j 37m 13s Dec -27� 41' 04'')

The galaxy in the foreground should, according to the accepted view of gravitational lensing, cause some distortion of the image of the galaxy in the background, a clear contradiction to the current models for the condition for gravitational lensing.

	Fig 9a
	Fig 9b
	Fig 9c

Fig 9  Typically Accepted Models thought to be Requirements for Lensing

from the European Space Agency: www.spacetelescope.org/.../medium/heic0113d.jpg

This is obviously a contradiction to the above Galaxy Pair NGC 3314

The lensing requirement suggested in Fig 9 is an obvious contradiction to the above image in Fig 8 on the Galaxy Pair NGC 3314. 

Fig 9a represents a hypothetical Einstein ring due to the lensing of a point-like mass in the foreground of the light emitted from a background source.

Fig 9b represents an Einstein cross, a serious contradiction to fundamental concepts on gravitational lensing. It is hypothesized by the researchers that point-like gravitating masses contained within a spiral galaxy PGC 69457 caused the light from a single quasar light source to be split up four ways. The images collected since 1990 show no changes with times. There is no evidence of relative motion between the hypothesized lensing masses within the PGC 69457 spiral galaxy. Any closely packed super massive objects will have to have some gravitational interaction with one another and thus, some relative motion. The optical lensing fundamentals would have to be stretched somewhat drastically in order to support any theory that explains a quadruple image of a single light source by a compact region of point-like gravitating masses contained within a spiral galaxy as imaged in Fig 9b. 

Fig 9c represents multiple lensing producing images of a single light source. This would require an ideal condition for massive particles of a multiple lensing system to be set up in a compact region of space. Here again some fundamentals would have to be violated or modified.

The stellar sky presents vast opportunities to modern Astronomy and Astrophysics to allow the detection of lensing events due to the large numbers of stellar objects that just happen to be positioned in a near perfect line-of-site to the earth based observers; again of course, assuming the validity of the light bending rule of General Relativity. With this in mind the entire celestial sky should be full of Einstein-rings!

Fig 10A Nearly edge-on view of Sombrero Galaxy, Reference: chandra.havard.edu

The Sombrero Galaxy is believed to have a super-massive black hole residing at its nucleus. The black hole is estimated to have a colossal mass on the order of 10⁹ solar masses. IMPORTANT: In order to us to be able to visualize the circular features of the outer rim of the Sombrero galaxy, the light coming from the far edge of this disc MUST pass over the super massive nucleus of this galaxy in order to arrive at our Earth based observatories.

Fig 10B Sombrero's  Bulge-Stars plugged into a Gaussian Sphere: A Light Bending Analysis

Let us include the enormous mass of the stars enclosed within an analytics Gaussian sphere that is concentric with the Sombrero nucleus with a radius such that it just barely touches the light rays coming from the far edges of the galaxy. This should suffice for a good estimate and we will barely need any calculations. If we plugged only one solar mass plugged into a Gaussian sphere of one solar radius, this would return a value of $8.48273 x 10^-6  radians or 1.75 arcsec. The Sombrero galaxy has a diameter of 50,000 light years and is tilted only 6 degrees, about 5000 light years from top to bottom edges of the galactic disc. So the light coming from the far edges must pass over the super massive bulge of Sombrero's nucleus, passing to within 2500 light years of the galactic nucleus. So our Gaussian sphere containing all those stars will have a radius of 2500 light years. Since the sun's radius is only 696,000 km or 2.32 light-seconds or just 7.3567 x 10^-8 light-years, our Gaussian sphere would have a radius of roughly 3.4 x 10¹⁰ solar radii. Now, Sombrero's super-massive black hole alone is estimated to have roughly 10⁹ solar masses. If the galactic bulge of Sombrero were estimated to contain 100 billions of stars, then our Gaussian sphere containing the galactic bulge of Sombrero must enclose at least 100 x 10⁹ solar masses alone. Thus, the mass of the stars enclosed in the Gaussian sphere containing the total mass of Sombrero's bulge would contribute a gravitational light bending effect many orders of magnitude greater than that of the sun.

Since any picture is worth a thousand words, we shall leave the images above, Figures 9 a, b and c, and Figures 10 A, B, C and D for discussions and Gedankenexperimente, a favorite technique of Dr Albert Einstein.

Fig 11 Undistorted time resolved images of stellar objects orbiting about Sagittarius A*

recorded processed images collected from 1992 to 2006

by

Max-Planck-Institut f�r extraterrestrische Physik

For details:

An Astrophysical Experiment that Relativity apparently Fails

under intense observations since 1992

The mathematical proof with illustrations of the emission theory that predicts these effects are published in a book which pertains to an emission theory; a principle of Mathematical Physics coined as the Extinction Shift Principle. The book, "Discourses & Mathematical Illustrations pertaining to the Extinction Shift Principle under the Electrodynamics of Galilean Transformations", contains the complete set of problems responsible for the success and fame of Relativity, worked out in Euclidean Space solely under Galilean Transformations of velocities. The principle correctly predicts the experimental outcome of important experiments of the past century. Astrophysical phenomena such as the planet Mercury and the PSR1913+16 neutron pulsar system perihelion rotation effects are calculated using pure classical procedures in Euclidean space. This emission theory predicts there can be NO direct interaction between Gravitation and Electromagnetism. For more details see the link: http://www.extinctionshift.com/topic_06.htm

Details on the Book: http://www.extinctionshift.com/Books.htm